binzume.net / 書庫 / ロボ研用資料 /

マイコンによるロボット制御::ロータリーエンコーダとか

ロボコンでロボットを目的地まで導くために，ライントレースと並んで重要なのがロータリーエンコーダです．

タイヤに取り付けたロータリーエンコーダの回転数から，自分の現在地を割り出します．

以下，後日．

ロータリーエンコーダの仕組み

ロータリーエンコーダには，大きく分けてインクリメンタル方式とアブソリュート方式があります．ロータリーエンコーダの性能は，一回転に何パルス出力するかで決まります．一回転のパルス数が多いほうが解像度が高いことになります．解像度が高いもので数千パルスのようです．マイコンで処理する場合，解像度の高いエンコーダをぐるぐる回すと秒間数万パルス以上の入力が入ることになるので処理の重さも考えたほうが良いと思います．

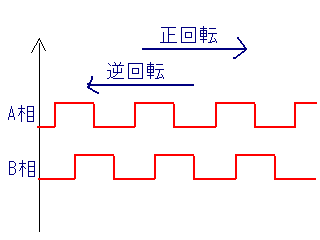
インクリメンタル方式とは，一定角度回転するごとにパルスが出るようになっています．B相，A相という位相がずれた２つの信号によって，回転方向もわかるようになっています．ボール式のマウス(注１)を分解したことがある人なら，「あぁ，あれか」と思うでしょう．基準点が分かるように，もう一本の信号線が出ているものもあるようです．

images/enc_fig1.png

アブソリュート方式は基準となる位置からの絶対角が２進数で得られます．まぁ，名前のままですね．

images/enc_fig2.png

インクリメンタル式のものが安いです．

ロータリーエンコーダを作る

精度を求めるなら止めて置いたほうが吉です．16パルス程度のものなら問題無いと思いますが……．

あまり解像度を上げると，位相が90度ずれるように調整するのが面倒になってきます．

マイコンへの入力

ピンへの信号の変化で割り込みが掛けられるなら，それを使った方がポーリングする必用がなくなって楽です．

割り込みに使えるピンが少ない場合は，B相とA相の排他的論理和(XOR)を取ったものをどちらかの入力と置き換えます．XORの結果を割り込みようのピンに繋げば，A相とB相のどちらかが変化すれば割り込みが掛かります．XORをとったことで情報が欠落することはありませんし，むしろ計算は楽になると思います．このとき，マイコンとXORで閾値が微妙に違うことも考えられるので，前もってシュミット回路で波形を整形する必要があります．

A(もしくはB)を上１ビット，A xor Bを下１ビットとしてみれば，00→01→10→11→00→01…というように２桁の２進数とみなせます．逆回転しているときは，逆向きに変化します．また，一度に２以上変化した場合は何かおかしいので無視するべきです．

計算方法

まず，構造体や定数を定義します．

#define PI 3.14159 // 円周率
#define ENCODER_DISTANCE 400 // 左右エンコーダ間の距離(mm)
#define ENCODER_STEP 250  // エンコーダの一ステップあたりの距離(0.01mm)
#define TURN_COUNT (ENCODER_DISTANCE*PI*2*100/ENCODER_STEP) // ロボットが一回転したときのカウント

struct ENC{
	int tmp_len,tmp_deg,tmp_x,tmp_y;
	int length; // 走行距離(無くても良い？)
	int x,y; // x,y座標(mm)
	int d; // 方向
}

実際のプログラムを書く予定ですが，まだありません．

速度

まず，左右のエンコーダからの入力をr(t)とl(t)とします．ここでは，割り込みを面積１のインパルスと考えて普通に関数として書きます．こうすると，r(t)とl(t)は，左右のエンコーダの回転速度の関数とみなせます．

ロータリーエンコーダがロボットの左右についている場合，エンコーダの分解能が十分ならば，ある瞬間のロボットの移動速度は，

v(t)=(r(t)+l(t))/2

となります．ただし，これは割り込みが入った瞬間にしか移動していないとみなされてしまうので，実際には一定時間内に進んだ距離から求めた方が楽でしょう．

進んだ距離

進んだ距離は単に加算(または減算)していけばいいだけです．ロボット自体が進んだ距離は，左右のエンコーダのカウントの平均を取ればいいです．

R(t)=∫r(t)dt (t=0～T)

L(t)=∫l(t)dt (t=0～T)

自分が現在向いている方向

少し考えてみると，左右のエンコーダのカウンタの差が，ロボットが向いている角度に比例していることに気付きます．

θ(t)=α(R(t)-L(t))

一周を2πにするとか，360度にするとかしてもいいですが，割り算をすれば誤差が気になるし，掛け算をすればオーバーフローが気になるので，そのまま使うのも手です．もしくは，sinのテーブルの大きさに合わせて，512とか256にするのが良いかも知れません．

現在地の座標を計算する

速度を積分すれば位置が求まります．

x=∫v(t)*sin(θ(t))dt

y=∫v(t)*cos(θ(t))dt

実際には，割り込みがあるたびに座標に加算していきます．三角関数が分かれば問題無いでしょう．

誤差を少なくするために

マイコンで計算する場合，sinやcosの値を定数倍しておいて，整数のみで固定小数点演算すると思いますが，誤差を少なくするために，乗除算のタイミングに気を使う必用があります．

終わりに

まだ校正中です．そのうちグラフや図を書きます．

この文書の履歴

Copyright © binzume all rights reserved.